When I wrote both of my blog posts on increasing performance through code profiling, I linked to a blog post that measured function call overhead from Python 3.5 to 3.8. That post was enlightening, but it was written in 2020 and significant effort has gone into improving CPython. Since the phrase "function calls are expensive" now lives rent-free in my head, I began to wonder how much of that post still holds up.
Testing Setup
I used a Rasperry Pi as the computer for my experiments, a 3B-non-plus model with a quad-core 1.2GHz processor I boot using a USB3-SATA adapter that gives me constant undervolting issues. I chose 64-bit Alpine 3.19.0 for the OS based on the lack of extraneous processes running by default; I installed the OS fresh and updated all the base system packages before testing, and made no tweaks to the boot config for additional performance. For the Python interpreter, I used the most recent version of the three most recent minor releases available in Alpine packages: 3.9.18, 3.10.13 and 3.11.6.
I chose to run this test on old, slow hardware because I have a bug up my butt about modern developers relying on super-fast modern hardware to conceal their inability to write performant code and wanted to minimize the effect of hardware assistance; I'll save my rant about how nobody writing JavaScript has heard of a profiler and it shows for another post.
Testing Methodology
The original post used empty functions to capture the overhead of a function call directly, but I believe using a function that performs an actual task will yield a more useful real-world result even if doing so requires comparisons to be relative instead of absolute.
I settled on converting integers to Roman numerals as my test function, writing the first version recursively to generate function calls:
def rn_recursive(num):
if num >= 1000:
return "M" + rn_recursive(num - 1000)
elif num >= 900:
return "CM" + rn_recursive(num - 900)
elif num >= 500:
return "D" + rn_recursive(num - 500)
elif num >= 400:
return "CD" + rn_recursive(num - 400)
elif num >= 100:
return "C" + rn_recursive(num - 100)
elif num >= 90:
return "XC" + rn_recursive(num - 90)
elif num >= 50:
return "L" + rn_recursive(num - 50)
elif num >= 40:
return "XL" + rn_recursive(num - 40)
elif num >= 10:
return "X" + rn_recursive(num - 10)
elif num >= 9:
return "IX" + rn_recursive(num - 9)
elif num >= 5:
return "V" + rn_recursive(num - 5)
elif num >= 4:
return "IV" + rn_recursive(num - 4)
elif num >= 1:
return "I" + rn_recursive(num - 1)
else:
return ""
I then rewrote the function iteratively as a control, taking care to replicate the recursive code flow as much as possible:
def rn_loop(num):
result = ""
while num > 0:
if num >= 1000:
result += "M"
num -= 1000
continue
if num >= 900:
result += "CM"
num -= 900
continue
if num >= 500:
result += "D"
num -= 500
continue
if num >= 400:
result += "CD"
num -= 400
continue
if num >= 100:
result += "C"
num -= 100
continue
if num >= 90:
result += "XC"
num -= 90
continue
if num >= 50:
result += "L"
num -= 50
continue
if num >= 40:
result += "XL"
num -= 40
continue
if num >= 10:
result += "X"
num -= 10
continue
if num >= 9:
result += "IX"
num -= 9
continue
if num >= 5:
result += "V"
num -= 5
continue
if num >= 4:
result += "IV"
num -= 4
continue
if num >= 1:
result += "I"
num -= 1
continue
return result
Once both functions were ready I began the experiment, 100 runs of each function converting the same number 100 times: [1]
recursive_times = {}
loop_times = {}
recursive_log = Path.home().joinpath("recursive.times")
loop_log = Path.home().joinpath("loop.times")
for i in range(1, 4000):
loop_timer = Timer(
stmt = f"rn_loop({i})",
setup = "from __main__ import rn_loop",
timer = process_time_ns
)
recursive_timer = Timer(
stmt = f"rn_recursive({i})",
setup = "from __main__ import rn_recursive",
timer = process_time_ns
)
loop_times[i] = loop_timer.repeat(number = 100, repeat = 100)
recursive_times[i] = recursive_timer.repeat(number = 100, repeat = 100)
recursive_log.write_text(dumps(recursive_times))
loop_log.write_text(dumps(loop_times))
Analysis
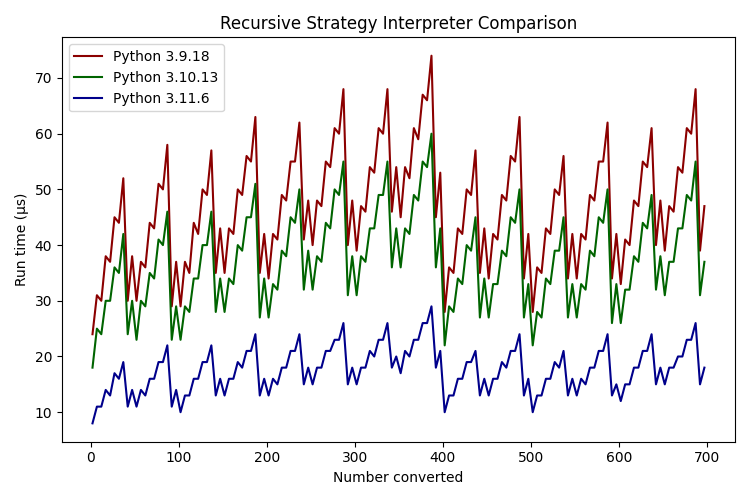
I was going to go full data science with standard deviations and stuff but instead followed the suggestion in the Python docs to focus on the minimum value from each run. I'll begin with the overall comparisons:
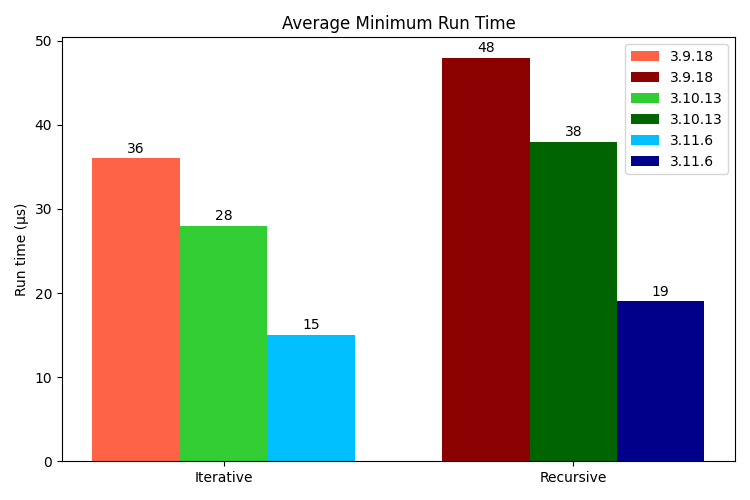
Average Minimum Run Times
| Python Version | Iterative (μs) | Recursive (μs) |
|---|---|---|
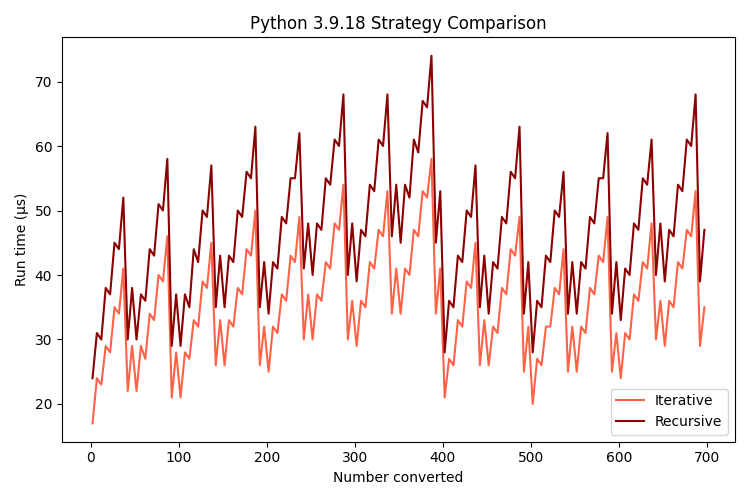
| 3.9.18 | 36.237 | 48.444 |
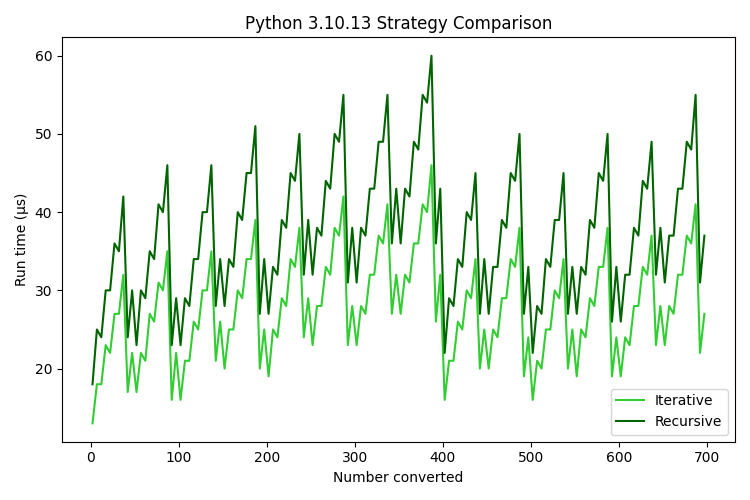
| 3.10.13 | 28.234 | 38.967 |
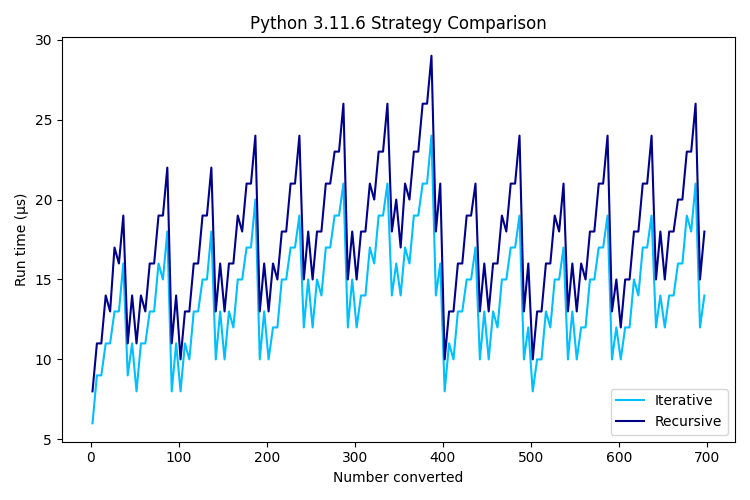
| 3.11.6 | 15.452 | 19.497 |
The average minimum run time is the mean of the fastest 100-run test for each number converted - the fastest 100-run test to convert the number 1, averaged with the fastest 100-run test to convert the number 2, etc. All run times are averaged before the mean is normalized to a single run and converted to microseconds.
The preferable strategy is apparent from this comparison: iterative runs take 74% the time of recursive runs on Python 3.9, 72% the time on Python 3.10 and 79% the time on Python 3.11.
An unexpected surprise is the benefit of a newer interpreter: iterative runs take 77% the time and recursive runs take 80% the time after upgrading from 3.9 to 3.10; after upgrading from 3.10 to 3.11 iterative and recursive runs take 54% and 50% the time respectively.
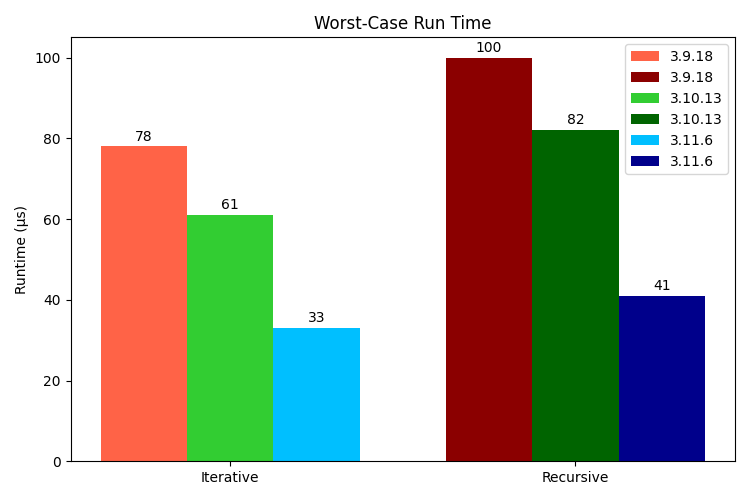
Worst-Case Average Run Times
| Python Version | Iterative (μs) | Recursive (μs) |
|---|---|---|
| 3.9.18 | 78.751 | 100.638 |
| 3.10.13 | 61.675 | 82.254 |
| 3.11.6 | 33.938 | 41.434 |
The worst-case average run time is the mean of all runs of the number with the largest minimum run time; the mean is normalized to a single run and converted to microseconds. [2]
I would have expected the iterative strategy to increase its lead over the recursive strategy in the worst case, but the gap tightened slightly: iterative runs took 78%, 74% and 81% the time of recursive runs on Python 3.9, 3.10 and 3.11 respectively.
The upgraded interpreter runtime benefit was also reduced in the worst case, but slightly less than the inter-strategy benefit: iterative runs take 78% the time and recursive runs take 81% the time after upgrading from 3.9 to 3.10; they respectively take 55% and 50% the time after upgrading from 3.10 to 3.11.
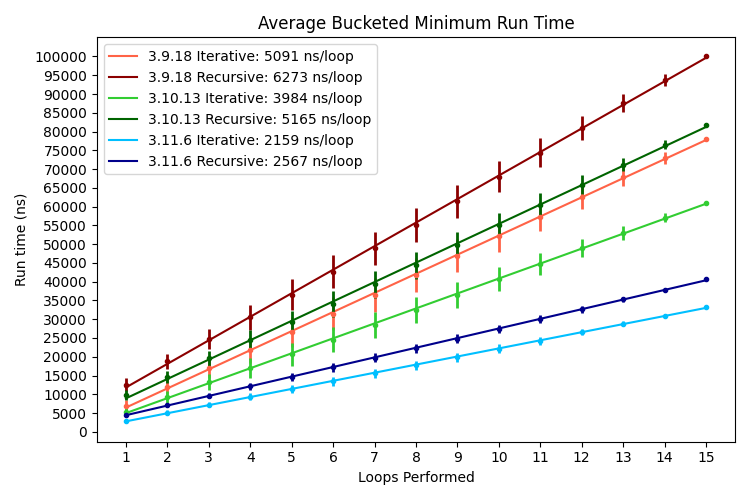
Average Bucketed Minimum Run Times
| Loops Performed | 3.9.18 Iterative (ns) | 3.9.18 Recursive (ns) | 3.10.13 Iterative (ns) | 3.10.13 Recursive (ns) | 3.11.6 Iterative (ns) | 3.11.6 Recursive (ns) |
|---|---|---|---|---|---|---|
| 1 | 6873 | 12603 | 5381 | 9823 | 2779 | 4566 |
| 2 | 12032 | 18764 | 9352 | 14671 | 5145 | 7128 |
| 3 | 16955 | 24669 | 13261 | 19547 | 7274 | 9643 |
| 4 | 21715 | 30525 | 16936 | 24336 | 9312 | 12121 |
| 5 | 26508 | 36530 | 20658 | 29162 | 11387 | 14648 |
| 6 | 31436 | 42610 | 24489 | 34096 | 13464 | 17159 |
| 7 | 36563 | 48872 | 28433 | 39251 | 15610 | 19700 |
| 8 | 41699 | 55111 | 32418 | 44346 | 17738 | 22271 |
| 9 | 46901 | 61469 | 36530 | 49720 | 19917 | 24826 |
| 10 | 52109 | 67918 | 40703 | 55057 | 22132 | 27458 |
| 11 | 57292 | 74360 | 44797 | 60475 | 24306 | 30013 |
| 12 | 62598 | 80961 | 48968 | 65845 | 26572 | 32665 |
| 13 | 67881 | 87567 | 53053 | 71215 | 28746 | 35312 |
| 14 | 72968 | 93800 | 57008 | 76532 | 30940 | 37822 |
| 15 | 77972 | 100202 | 61043 | 81861 | 33215 | 40619 |
The average bucketed minimum run time is the mean of the smallest run time for each number requiring a given number of loops for conversion - the minimum run times for the numbers 1, 4, 5, 9, 10, 40, 50, 90, 100, 400, 500, 900 and 1000 are averaged together as they can all be converted in one loop, and so on. All run times are averaged before the mean is normalized to a single run.
The graph shows the amount of time needed to complete a single run appears to increase linearly with the number of loops for each strategy and interpreter, with the data points hewing very close to the trend line; I believe this suggests there was little outside effect during testing, although the somewhat large error bars do raise an eyebrow.
While the fact the iterative strategies are faster than the recursive strategies everywhere is unsurprising, one new piece of information is the difference between the strategies widens as the number of loops increases - this surprised me so I dug into it more:
| Loops Performed | 3.9.18 (ns) | 3.10.13 (ns) | 3.11.6 (ns) |
|---|---|---|---|
| 1 | 5730 | 4442 | 1787 |
| 2 | 6732 | 5319 | 1983 |
| 3 | 7714 | 6286 | 2369 |
| 4 | 8810 | 7400 | 2809 |
| 5 | 10022 | 8504 | 3261 |
| 6 | 11174 | 9607 | 3695 |
| 7 | 12309 | 10818 | 4090 |
| 8 | 13412 | 11928 | 4533 |
| 9 | 14568 | 13190 | 4909 |
| 10 | 15809 | 14354 | 5326 |
| 11 | 17068 | 15678 | 5707 |
| 12 | 18363 | 16877 | 6093 |
| 13 | 19686 | 18162 | 6566 |
| 14 | 20832 | 19524 | 6882 |
| 15 | 22230 | 20818 | 7404 |
The average bucketed minimum run time difference is the difference between the iterative and recursive means for each interpreter - the first graph was a bit cluttered so I made a second to highlight this difference. While the average bucketed minimum run time graph shows how much faster Python 3.11 is to the older versions, this graph shows how much tighter Python 3.11 execution is with each additional loop requiring almost a third the runtime of the other two versions.
I believe this graph is the most important to my hypothesis as the code paths between the iterative and recursive strategies are so similar that taking their difference should leave only the implicit differences, which should only be the function calls from recursion.
One additional piece of information this graph provides is the difference between run times on Python 3.9 and 3.10 appears to be more of a shallow parabola than linear, while Python 3.11 appears to remain linear. If this is the case, it suggests a recursive strategy may be even worse with these versions than initially expected.
Conclusion
So after all this effort, did I manage to prove function calls were the primary factor behind the decreased performance of the recursive strategy? I believe I did: the test functions were similar enough to make differing code path issues unlikely; the test environment was isolated and built specifically for this experiment to minimize noise; and finally the test data trends replicated across interpreter versions. [3]
Barring the possibility of me completely missing something incredibly obvious, I believe the average bucketed minimum run time difference shows the effect of additional function calls and I can now say it's faster to write code in an iterative style and inline small functions where possible. [4]
Appendix
While writing my conclusion, I realized the recursive function creates new integer objects to pass around and that overhead will show up in my data even though it isn't strictly part of a function call; then I remembered both that the substantial bucketed run time differences at a loop value of 1 suggests the difference cannot come from integer creation alone and that the trend still held at small integers even though Python interns small integers preventing new integer object creation.
As a sanity check, I compared the minimum run times for two groups of integers that required the same number of loops to convert: ones that should be interned by Python (188, 238) and ones that shouldn't (3707, 3998); somehow the integers that weren't interned had significantly lower minimum run times. I don't know why this would be the case but I have spent too much time on this post already and want to do something else - have a collection of graphs I couldn't find a place for in lieu of me making this post even longer.
| [1] | I thought the natural smoothing of aggregating 100 runs would be beneficial; during analysis I wished I'd made 10000 individual runs instead |
| [2] | The most time-intensive number to convert is 3888, which is a bit strange until you think about it |
| [3] | I suppose I could throw the functions into a disassembler and read the Python bytecode to confirm the code paths are similar, but I've spent too much time on this post already |
| [4] | Will the code maintain its readability and maintainability after doing these things? Who can say |